Due on Dec 3 (20 points)

1. (5 points) Consider a binary channel with a cross over probability of 0.15 and an erasure probability of 0.1, what is the capacity of the channel? In other words, when a bit is sent through the channel, there is a probability of 0.15 that the bit is flipped, a probability of 0.1 that the bit got erased (the decoder can't even tell if the received bit is 0 or 1), and a probability of 0.75 that the bit is transmitted correctly.

2. (10 points) Prove the Cauchy-Schwarz inequality \(E[X^2]E[Y^2]\ge E[XY]^2\). (Hint: note that \(E[(X-\lambda Y)^2] \ge 0\) and find \(\lambda\) that minimizes \(E[(X-\lambda Y)^2]\)).

3. (5 points) For the simple Bayesian network below,

   1. Identify a pair of independent variables

   2. Identify a pair of conditionally independent variables given some variables

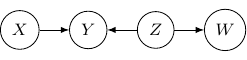Extra-credits:

1. (5 points) Consider a channel composed of two parallel Gaussian channels with noise powers \({N_1}=1\) and \({N_2}=5\). Given a total power \(P\), you may assign power \(P_1\) to channel 1 and power \(P_2\) to channel 2 such that \(P_1+P_2=P\). By trading off the power between the two channels, compute the (maximum) overall capacity: \(\frac{1}{2} \log(1+\frac{P_1}{N_1}) + \frac{1}{2} \log(1+\frac{P_2}{N_2}\)) for

   1. \(P = 13\)

   2. \(P = 3\)

2. (5 points) For the above question, find a general expression of the overall capacity for any \(P\).

3. Consider the problem of estimating the variance of a zero-mean Gaussian random variable \(X\sim \mathcal{N}(0,\nu)\) from \(N\) samples, where \(\nu\) is the variance of \(X\).

   1. (10 points) Find the Cramar-Rao Lower Bound (CRLB) for the unbiased estimators.

   2. (10 points) Propose an unbiased estimator and prove its optimality by showing that the variance of the estimate achieves the CRLB.

4. (10 points) Try to repeat Q1 in the midterm using Lea (or any other probabilistic programming tool).